Optimal Trajectories for Multiple-UAS Simultaneous Target Acquisition with Obstacle Avoidance
Abstract
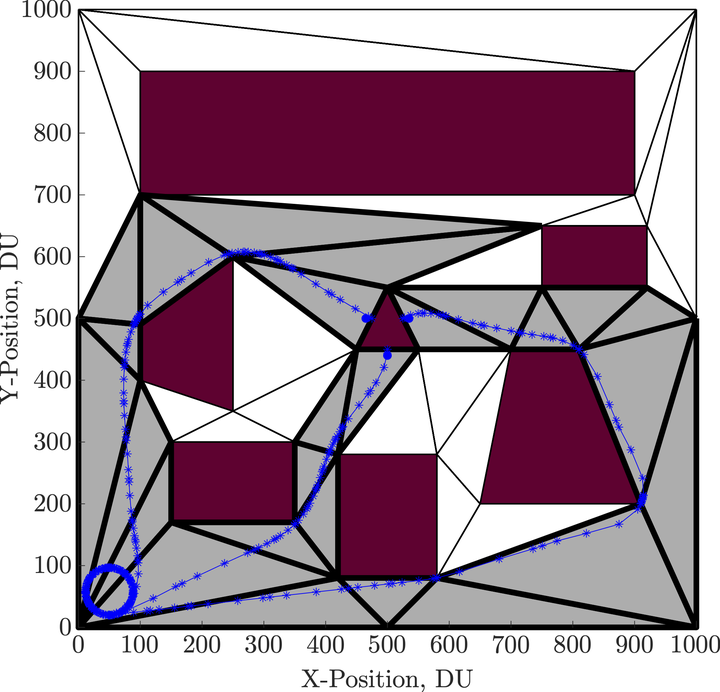
This work develops feasible path trajectories for a coordinated strike with multiple aircraft in a constrained environment. Using direct orthogonal collocation methods, the two-point boundary value optimal control problem is transcribed into a nonlinear programming problem. A coordinate transformation is performed on the state variables to leverage the benefits of a simplex discretization of the search domain. Applying these techniques allows each path constraint to be removed from the feasible search space, eliminating computationally expensive, nonlinear constraint equations and problem specific parameters from the optimal control formulation. Heuristic search techniques are used to determine a Dubins path solution through the space to seed the optimal control solver. In the scenario, three aircraft are initiated in separate directions and are required to avoid all constrained regions while simultaneously arriving at the target location, each with a different viewing angle. A focus of this work is to reduce computation times for optimal control solvers such that real-time solutions can be implemented onboard small unmanned aircraft systems. Analysis of the problem examines optimal flight paths through simplex corridors, velocity and heading vectors, control vectors of acceleration and heading rate, and objective times for minimum time flight.